本文参考:数据结构(c语言版) 李云清等编著、算法导论
引言:
在文本编辑中,我们经常要在一段文本中某个特定的位置找出 某个特定的字符或模式。
由此,便产生了字符串的匹配问题。
本文由简单的字符串匹配算法开始,再到KMP算法,由浅入深,教你从头到尾彻底理解KMP算法。
来看算法导论一书上关于此字符串问题的定义:
假设文本是一个长度为n的数组T[1...n],模式是一个长度为m<=n的数组P[1....m]。
进一步假设P和T的元素都是属于有限字母表Σ.中的字符。
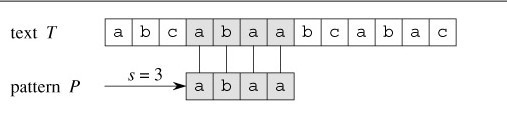
依据上图,再来解释下字符串匹配问题。目标是找出所有在文本T=abcabaabcaabac中的模式P=abaa所有出现。
该模式仅在文本中出现了一次,在位移s=3处。位移s=3是有效位移。
第一节、简单的字符串匹配算法
简单的字符串匹配算法用一个循环来找出所有有效位移,
该循环对n-m+1个可能的每一个s值检查条件P[1....m]=T[s+1....s+m]。
NAIVE-STRING-MATCHER(T, P)
1 n ← length[T]
2 m ← length[P]
3 for s ← 0 to n - m
4 do if P[1 ‥ m] = T[s + 1 ‥ s + m]
//对n-m+1个可能的位移s中的每一个值,比较相应的字符的循环必须执行m次。
5 then print "Pattern occurs with shift" s

简单字符串匹配算法,上图针对文本T=acaabc 和模式P=aab。
上述第4行代码,n-m+1个可能的位移s中的每一个值,比较相应的字符的循环必须执行m次。
所以,在最坏情况下,此简单模式匹配算法的运行时间为O((n-m+1)m)。
--------------------------------
下面我再来举个具体例子,并给出一具体运行程序:
对于目的字串target是banananobano,要匹配的字串pattern是nano,的情况,
下面是匹配过程,原理很简单,只要先和target字串的第一个字符比较,
如果相同就比较下一个,如果不同就把pattern右移一下,
之后再从pattern的每一个字符比较,这个算法的运行过程如下图。
//index表示的每n次匹配的情形。

#include<iostream>
#include<string>
using namespace std;
int match(const string& target,const string& pattern)
{
int target_length = target.size();
int pattern_length = pattern.size();
int target_index = 0;
int pattern_index = 0;
while(target_index < target_length && pattern_index < pattern_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else
{
target_index -= (pattern_index-1);
pattern_index = 0;
}
}
if(pattern_index == pattern_length)
{
return target_index - pattern_length;
}
else
{
return -1;
}
}
int main()
{
cout<<match("banananobano","nano")<<endl;
return 0;
}
//运行结果为4。
上面的算法进间复杂度是O(pattern_length*target_length),
我们主要把时间浪费在什么地方呢,
观查index =2那一步,我们已经匹配了3个字符,而第4个字符是不匹配的,这时我们已经匹配的字符序列是nan,
此时如果向右移动一位,那么nan最先匹配的字符序列将是an,这肯定是不能匹配的,
之后再右移一位,匹配的是nan最先匹配的序列是n,这是可以匹配的。
如果我们事先知道pattern本身的这些信息就不用每次匹配失败后都把target_index回退回去,
这种回退就浪费了很多不必要的时间,如果能事先计算出pattern本身的这些性质,
那么就可以在失配时直接把pattern移动到下一个可能的位置,
把其中根本不可能匹配的过程省略掉,
如上表所示我们在index=2时失配,此时就可以直接把pattern移动到index=4的状态,
kmp算法就是从此出发。
第二节、KMP算法
2.1、 覆盖函数 (overlay_function)
覆盖函数所表征的是pattern本身的性质,可以让为其表征的是pattern从左开始的所有连续子串的自我覆盖程度。
比如如下的字串,abaabcaba
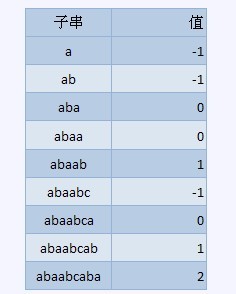
由于计数是从0始的,因此覆盖函数的值为0说明有1个匹配,对于从0还是从来开始计数是偏好问题,
具体请自行调整,其中-1表示没有覆盖,那么何为覆盖呢,下面比较数学的来看一下定义,比如对于序列
a 0 a 1... a j-1 a j
要找到一个 k, 使它满足
a 0 a 1... a k-1 a k= a j-k a j-k+1... a j-1 a j
而没有更大的k满足这个条件,就是说要找到尽可能大k,使pattern前k字符与后k字符相匹配,k要尽可能的大,
原因是如果有比较大的k存在,而我们选择较小的满足条件的k,
那么当失配时,我们就会使pattern向右移动的位置变大,而较少的移动位置是存在匹配的,这样我们就会把可能匹配的结果丢失。
它本质上是找到即是模式串p的前缀,又是它的后缀的最长字符串。
比如下面的序列,
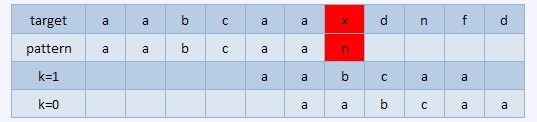
在红色部分失配,正确的结果是k=1的情况,把pattern右移4位,如果选择k=0,右移5位则会产生错误。
计算这个overlay函数的方法可以采用递推,可以想象如果对于pattern的前j个字符,如果覆盖函数值为k
a 0 a 1... a k-1 a k= a j-k a j-k+1... a j-1 a j
则对于pattern的前j+1序列字符,则有如下可能
⑴ pattern[k+1]==pattern[j+1] 此时overlay(j+1)=k+1=overlay(j)+1
⑵ pattern[k+1]≠pattern[j+1] 此时只能在pattern前k+1个子符组所的子串中找到相应的overlay函数,h=overlay(k),如果此时pattern[h+1]==pattern[j+1],则overlay(j+1)=h+1否则重复(2)过程.
下面给出一段计算覆盖函数的代码:
#include<iostream>
#include<string>
using namespace std;
void compute_overlay(const string& pattern)
{
const int pattern_length = pattern.size();
int *overlay_function = new int[pattern_length];
int index;
overlay_function[0] = -1;
for(int i=1;i<pattern_length;++i)
{
index = overlay_function[i-1];
//store previous fail position k to index;
while(index>=0 && pattern[i]!=pattern[index+1])
{
index = overlay_function[index];
}
if(pattern[i]==pattern[index+1])
{
overlay_function[i] = index + 1;
}
else
{
overlay_function[i] = -1;
}
}
for(i=0;i<pattern_length;++i)
{
cout<<overlay_function[i]<<endl;
}
delete[] overlay_function;
}
int main()
{
string pattern = "abaabcaba";
compute_overlay(pattern);
return 0;
}
运行结果为:
-1
-1
0
0
1
-1
0
1
2
Press any key to continue
-------------------------------------
2.2、kmp算法
有了覆盖函数,那么实现kmp算法就是很简单的了,我们的原则还是从左向右匹配,但是当失配发生时,我们不用把target_index向回移动,target_index前面已经匹配过的部分在pattern自身就能体现出来,只要动pattern_index就可以了。
当发生在j长度失配时,只要把pattern向右移动j-overlay(j)长度就可以了。
如果失配时pattern_index==0,相当于pattern第一个字符就不匹配,
这时就应该把target_index加1,向右移动1位就可以了。
ok,下图就是KMP算法的过程(红色即是采用KMP算法的执行过程):
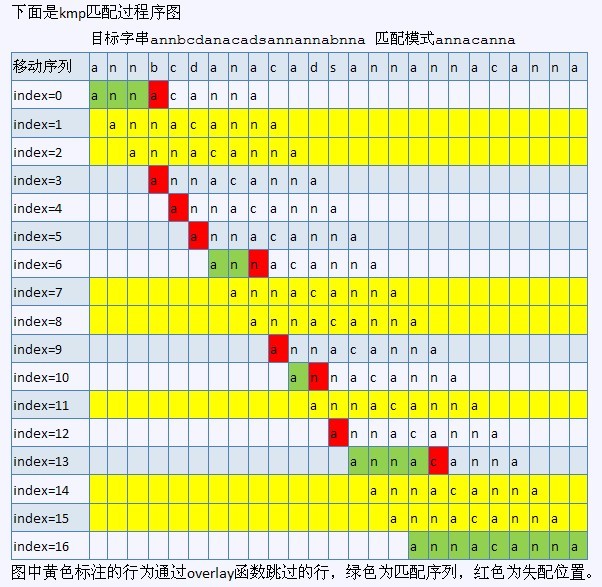
另一作者saturnman发现,在上述KMP匹配过程图中,index=8和index=11处画错了。还有,anaven也早已发现,index=3处也画错了。非常感谢。但图已无法修改,见谅。
KMP 算法可在O(n+m)时间内完成全部的串的模式匹配工作。
ok,最后给出KMP算法实现的c++代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
int kmp_find(const string& target,const string& pattern)
{
const int target_length = target.size();
const int pattern_length = pattern.size();
int * overlay_value = new int[pattern_length];
overlay_value[0] = -1;
int index = 0;
for(int i=1;i<pattern_length;++i)
{
index = overlay_value[i-1];
while(index>=0 && pattern[index+1]!=pattern[i])
{
index = overlay_value[index];
}
if(pattern[index+1]==pattern[i])
{
overlay_value[i] = index +1;
}
else
{
overlay_value[i] = -1;
}
}
//match algorithm start
int pattern_index = 0;
int target_index = 0;
while(pattern_index<pattern_length&&target_index<target_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else if(pattern_index==0)
{
++target_index;
}
else
{
pattern_index = overlay_value[pattern_index-1]+1;
}
}
if(pattern_index==pattern_length)
{
return target_index-pattern_index;
}
else
{
return -1;
}
delete [] overlay_value;
}
int main()
{
string source = " annbcdanacadsannannabnna";
string pattern = " annacanna";
cout<<kmp_find(source,pattern)<<endl;
return 0;
}
//运行结果为 -1.
第三节、kmp算法的来源
kmp如此精巧,那么它是怎么来的呢,为什么要三个人合力才能想出来。其实就算没有kmp算法,人们在字符匹配中也能找到相同高效的算法。这种算法,最终相当于kmp算法,只是这种算法的出发点不是覆盖函数,不是直接从匹配的内在原理出发,而使用此方法的计算的覆盖函数过程序复杂且不易被理解,但是一但找到这个覆盖函数,那以后使用同一pattern匹配时的效率就和kmp一样了,其实这种算法找到的函数不应叫做覆盖函数,因为在寻找过程中根本没有考虑是否覆盖的问题。
说了这么半天那么这种方法是什么呢,这种方法是就大名鼎鼎的确定的有限自动机(Deterministic finite state automaton DFA),DFA可识别的文法是3型文法,又叫正规文法或是正则文法,既然可以识别正则文法,那么识别确定的字串肯定不是问题(确定字串是正则式的一个子集)。对于如何构造DFA,是有一个完整的算法,这里不做介绍了。在识别确定的字串时使用DFA实在是大材小用,DFA可以识别更加通用的正则表达式,而用通用的构建DFA的方法来识别确定的字串,那这个overhead就显得太大了。
kmp算法的可贵之处是从字符匹配的问题本身特点出发,巧妙使用覆盖函数这一表征pattern自身特点的这一概念来快速直接生成识别字串的DFA,因此对于kmp这种算法,理解这种算法高中数学就可以了,但是如果想从无到有设计出这种算法是要求有比较深的数学功底的。
第四节、 精确字符匹配的常见算法的解析
KMP 算法:
KMP 就是串匹配算法
运用自动机原理
比如说
我们在 S 中找 P
设 P = {ababbaaba}
我们将 P 对自己匹配
下面是求的过程 :{ 依次记下匹配失败的那一位 }
[2]ababbaaba
....... a babbaaba[1]
[3]ababbaaba
......... a babbaaba[1]
[4]ababbaaba
.........a b abbaaba[2]
[5]ababbaaba
.........ab a bbaaba[3]
[6]ababbaaba
................ababbaaba[1]
[7]ababbaaba
................ababbaaba[2]
[8]ababbaaba
..................ababbaaba[2]
[9]ababbaaba
..................ababbaaba[3]
得到 Next 数组『 0,1,1,2,3,1,2,2,3 』
主过程:
[1]i:=1 j:=1
[2] 若 (j>m) 或 (i>n) 转 [4] 否则转 [3]
[3] 若 j=0 或 a[i]=b[j] 则【 inc(i)inc(j) 转 [2] 】否则【 j:=next[j] 转 2 】
[4] 若 j>m 则 return(i-m) 否则 return -1;
若返回- 1 表示失败,否则表示在 i-m 处成功
BM 算法也是一种快速串匹配算法, KMP 算法的主要区别是匹配操作的方向不同。虽然 T 右移的计算方法却发生了较大的变化。
为方便讨论, T =" dist :c->{ dist 称为滑动距离函数,它给出了正文中可能出现的任意字符在模式中的位置。函数 m – j j 为 dist ( m+1 若 c = tm
例如, pattern ",则 p ) a ) t ) dist ( = 2 , r ) n ) BM 算法的基本思想是:假设将主串中自位置 i + dist(si) 位置开始重新进行新一轮的匹配,其效果相当于把模式和主串向右滑过一段距离 si ),即跳过 si )个字符而无需进行比较。
下面是一个 S = " T= " BM 算法可以大大加快串匹配的速度。
下面是 KMP 算法部分,把调用 BM 函数便可。
- #include <iostream>
- using namespace std;
-
- int Dist( char *t, char ch)
- {
- int len = strlen(t);
- int i = len - 1;
- if (ch == t[i])
- return len;
- i--;
- while (i >= 0)
- {
- if (ch == t[i])
- return len - 1 - i;
- else
- i--;
- }
- return len;
- }
-
- int BM( char *s, char *t)
- {
- int n = strlen(s);
- int m = strlen(t);
- int i = m-1;
- int j = m-1;
- while (j>=0 && i<n)
- {
- if (s[i] == t[j])
- {
- i--;
- j--;
- }
- else
- {
- i += Dist(t,s[i]);
- j = m-1;
- }
- }
- if (j < 0)
- {
- return i+1;
- }
- return -1;
- }
Horspool 算法
这个算法是由 R.Nigel Horspool 在 1980 年提出的。其滑动思想非常简单,就是从后往前匹配模式串,若在某一位失去匹配,此位对应的文本串字符为 c ,那就将模式串向右滑动,使模式
串之前最近的 c 对准这一位,再从新从后往前检查。那如果之前找不到 c 怎么办?那好极了,直接将整个模式串滑过这一位。
例如:
文本串: abdabaca
模式串: baca
倒数第 2 位失去匹配,模式串之前又没有 d ,那模式串就可以整个滑过,变成这样:
文本串: abdabaca
模式串: baca
发现倒数第 1 位就失去匹配,之前 1 位有 c ,那就向右滑动 1 位:
文本串: abdabaca
模式串: baca
实现代码:
- #include <iostream>
- #include <vector>
- #include <string>
- #include <cstdlib>
- using namespace std;
-
- int Horspool_match( const string & S, const string & M, int pos)
- {
- int S_len = S.size();
- int M_len = M.size();
- int Mi = M_len-1,Si= pos+Mi;
- if ( (S_len-pos) < M_len )
- return -1;
- while ( (Mi>-1) && (Si<S_len) )
- {
- if (S[Si] == M[Mi])
- {
- --Mi;
- --Si;
- }
- else
- {
- do
- {
- Mi--;
- }
- while ( (S[Si]!=M[Mi]) || (Mi>-1) );
- Mi = M_len - 1;
- Si += M_len - 1;
- }
- }
- if (Si < S_len)
- return (Si + 1);
- else
- return -1;
- }
-
- int main( )
- {
- string S= "abcdefghabcdefghhiijiklmabc" ;
- string T= "hhiij" ;
- int pos = Horspool_match(S,T,3);
-
- cout<< "/n" <<pos<<endl;
- system( "pause" );
- return 0;
- }
SUNDAY 算法:
BM 算法的改进的算法 SUNDAY--Boyer-Moore-Horspool-Sunday Aglorithm
BM 算法优于 KMP
SUNDAY 算法描述:
字符串查找算法中,最著名的两个是 KMP 算法( Knuth-Morris-Pratt) 和 BM 算法( Boyer-Moore) 。两个算法在最坏情况下均具有线性的查找时间。但是在实用上, KMP 算法并不比最简单的 c 库函数 strstr() 快多少,而 BM 算法则往往比 KMP 算法快上 3 - 5 倍。但是 BM 算法还不是最快的算法,这里介绍一种比 BM 算法更快一些的查找算法即 Sunday 算法。
例如我们要在 "substring searching algorithm" 查找 "search" ,刚开始时,把子串与文本左边对齐:
substring searching algorithm
search
^
结果在第二个字符处发现不匹配,于是要把子串往后移动。但是该移动多少呢?这就是各种算法各显神通的地方了,最简单的做法是移动一个字符位置; KMP 是利用已经匹配部分的信息来移动; BM 算法是做反向比较,并根据已经匹配的部分来确定移动量。 这里要介绍的方法是看紧跟在当前子串之后的那个字符(上图中的 'i') 。
显然,不管移动多少,这个字符是肯定要参加下一步的比较的,也就是说,如果下一步匹配到了,这个字符必须在子串内。所以,可以移动子串,使子串中的最右边的这个字符与它对齐。现在子串 'search' 中并不存在 'i' ,则说明可以直接跳过一大片,从 'i' 之后的那个字符开始作下一步的比较,如下图:
substring searching algorithm
search
^
比较的结果,第一个字符就不匹配,再看子串后面的那个字符,是 'r', 它在子串中出现在倒数第三位,于是把子串向前移动三位,使两个 'r' 对齐,如下:
substring searching algorithm
search
^
哈!这次匹配成功了!回顾整个过程,我们只移动了两次子串就找到了匹配位置,可以证明,用这个算法,每一步的移动量都比 BM 算法要大,所以肯定比 BM 算法更快。
- #include<iostream>
- #include<fstream>
- #include<vector>
- #include<algorithm>
- #include<string>
- #include<list>
- #include<functional>
-
- using namespace std;
-
- int main()
- {
- char *text= new char [100];
- text= "substring searching algorithm search" ;
- char *patt= new char [10];
- patt= "search" ;
- size_t temp[256];
- size_t *shift=temp;
-
- size_t patt_size=strlen(patt);
- cout<< "size : " <<patt_size<<endl;
- for ( size_t i=0;i<256;i++)
- *(shift+i)=patt_size+1;
-
- for (i=0;i<patt_size;i++)
- *(shift+unsigned char (*(patt+i) ) )=patt_size-i;
-
-
-
-
- size_t text_size=strlen(text);
- size_t limit=text_size-i+1;
-
- for (i=0;i<limit;i+=shift[text[i+patt_size] ] )
- if (text[i]==*patt)
- {
-
-
-
-
-
-
-
- char * match_text=text+i+1;
- size_t match_size=1;
- do {
- if (match_size==patt_size)
-
- cout<< "the no is " <<i<<endl;
- } while ( (*match_text++)==patt[match_size++] );
- }
-
- cout<<endl;
- return 0;
- }
-
-
-
-
-
-
-
-
本文完,更多请参考: 六(续)、从KMP算法一步一步谈到BM算法 。